들어가며
소프트웨어는 다양한 데이터를 다루는 복잡한 시스템이다. 이러한 데이터는 단순히 숫자나 문자열로 표현되는 것이 아니라, 그 자체로 의미를 가지며, 이를 잘 이해하고 활용하는 것이 소프트웨어 개발의 핵심이다. 이번 글에서는 이러한 데이터의 양이나 크기를 정량적으로 표현하는 방법인 측도(Measure)에 대해 알아보겠다.
먼저 측도라는 단어가 생소하게 느껴질 수 있다. 측도는 데이터의 양이나 크기를 정량적으로 표현하는 방법을 말한다. 수학적으로는 개수, 길이, 넓이, 부피 등의 개념을 추상화한 것을 말한다. 예를 들어, 마리, 권, 그루, 다스와 같은 수량 개념부터 cm, kg, mL와 같은 단위, 달러나 엔과 같은 화폐까지 모두 측도의 일종이다. 좀 더 나아간다면 바퀴, 번과 같은 횟수 개념도 측도로 볼 수 있다.
이러한 측도는 비즈니스 관점에서 중요하다. 물건을 판매한다면 가격과 수량을 표현해야 하고, 글로벌 서비스를 한다면 다양한 화폐 단위를 다룰 수 있어야 한다. 또한, 단위 변환과 연산에 대한 고려도 필요하다. 예를 들어, 미국에서 판매되는 제품의 가격을 한국 원화로 변환해야 하거나, 세금이나 수수료 등을 고려하여 계산해줄 수도 있다.
추상화된 것을 구체화하기
우리는 숫자를 코드로 표현하고 싶을 때 Int나 Float와 같은 기본 자료형을 사용한다. 하지만 이러한 기본 자료형은 단순히 숫자일 뿐, 그 자체로 의미를 가지지 않는다. 예를 들어, 100이라는 숫자는 단순한 정수일 뿐이라 무게인지 길이인지 알 수 없다. 그래서 보통 다음과 같이 변수명에 의존하여 의미를 부여한다.
val weight: Int = 100 // 무게
val length: Int = 100 // 길이하지만 이러한 방식은 실수할 여지가 많다. Int라는 타입은 아무 숫자나 받을 수 있기 때문에, 잘못된 값을 넣을 수도 있다. 이를 방지하기 위해서 코드 리뷰나 테스트를 통해 확인할 수 있지만, 이런 단순한 문제로 생산성을 떨어뜨리는 것은 바람직하지 않다. 따라서 실수를 방지하기 위해 별도 타입을 만들 수 있다. 예를 들어, 무게를 표현하기 위해 Weight라는 클래스를 만들고, 이를 사용하여 무게를 표현할 수 있다.
class Weight(val value: Int) {
init {
require(value >= 0) { "Weight must be positive" }
}
}
val weight = Weight(100) // 무게위와 같이 Weight라는 클래스를 만들면, 무게를 표현할 때는 항상 Weight 타입을 사용해야 하므로 실수를 방지할 수 있다. 또한, 클래스에 다양한 연산을 추가하여 무게에 대한 연산을 쉽게 수행할 수 있다.
class Weight(val value: Int) {
init {
require(value >= 0) { "Weight must be positive" }
}
operator fun plus(other: Weight): Weight {
return Weight(value + other.value)
}
operator fun minus(other: Weight): Weight {
return Weight(value - other.value)
}
operator fun times(scalar: Int): Weight {
return Weight(value * scalar)
}
operator fun div(scalar: Int): Weight {
return Weight(value / scalar)
}
}
val weight1 = Weight(100)
val weight2 = Weight(200)
val totalWeight = weight1 + weight2 // 300
val halfWeight = weight1 / 2 // 50이러한 객체를 DDD(도메인 주도 설계)에서는 값 객체(Value Object)라고 부른다. 값 객체는 단순히 숫자나 문자열을 감싸는 것이 아니라, 그 자체로 의미를 가지는 객체를 말한다.
측도에 대한 모델링은 이런 개념에서 시작된다. 추상화된 값을 구체화하여 의미를 부여하고, 이를 통해 코드의 가독성을 높이고 실수를 방지하며, 비즈니스에 필요한 다양한 연산을 추가할 수 있다.
측도 모델링
앞서 구현한 값 객체를 이용할 수도 있지만, 조금 더 범용적으로 모델을 만드는 것도 가능하다. 단순히 무게나 길이와 같은 개별 타입을 만드는 것이 아니라, 모든 측도에 공통으로 적용할 수 있는 추상화된 모델을 구현해보자.
값과 단위
측도 시스템을 구현할 때 가장 기본이 되는 것은 '값(Value)'과 '단위(Unit)'의 개념이다. 모든 측도는 값과 단위의 조합으로 표현할 수 있다. 예를 들어 "5kg"는 값이 5이고 단위가 킬로그램인 측도이다.
그리고 단위는 연관성이 있는 단위들끼리 변환이 가능하다. 예를 들어 킬로그램(kg)과 그램(g)은 서로 변환이 가능하다. 이러한 단위 간의 변환을 지원하기 위해서는 별도로 단위계를 정의할 수 있어야 한다. 이와 같은 요구사항을 기반으로 다음과 같이 다이어그램을 그려볼 수 있다.
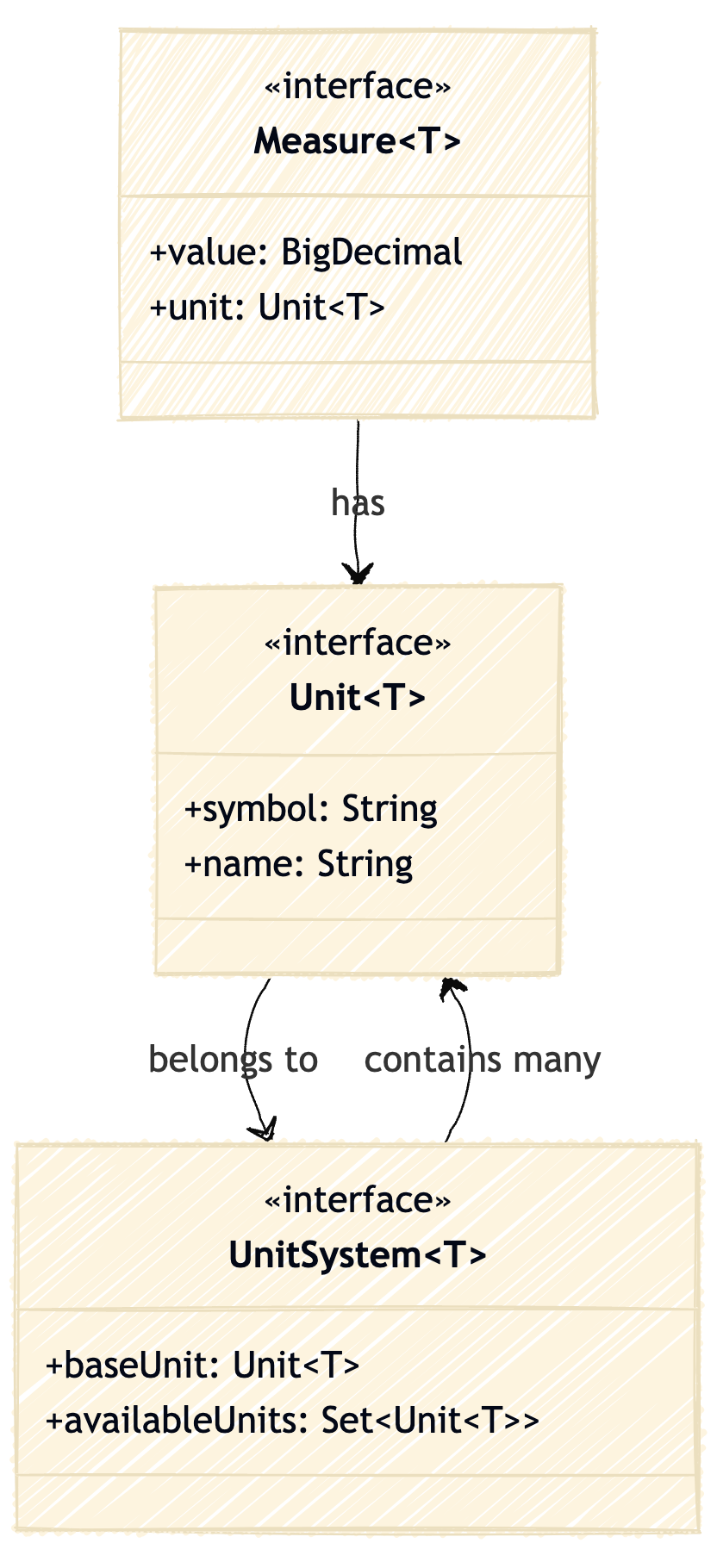
우리는 전체 측도 모델에 대한 기본 구조를 위와 같이 정의할 것이다. Measure는 모든 측도를 표현하는 모델이며, Unit�은 단위를 표현하는 모델이다. 그리고 UnitSystem은 특정 종류의 측도에 사용할 수 있는 모든 단위들의 집합을 관리하는 시스템이다. 이 구조를 기반으로 측도 모델을 구현해보자.
interface Measure<T : Measure<T>> : Comparable<T> {
val value: BigDecimal
val unit: MeasurementUnit<T>
fun convertTo(targetUnit: MeasurementUnit<T>): T
fun add(other: T): T
fun subtract(other: T): T
fun multiply(factor: BigDecimal): T
fun divide(divisor: BigDecimal): T
}위 코드에서 Measure 인터페이스는 T라는 제네릭 타입을 사용하며, 이는 자기 자신의 타입을 참조한다. 이러한 설계는 F-bounded polymorphism 패턴으로, 자기 자신의 타입을 참조하여 타입 안전성을 보장한다. 예를 들어 Weight라는 클래스가 Measure<Weight>를 구현한다면, add 메서드는 Weight 타입만 받을 수 있다.
또한 모든 측도는 Comparable을 구현하여 비교 가능하도록 했다. 예를 들어 "5kg"과 "3kg"를 비교하여 어느 것이 더 무거운지 판단할 수 있다.
다음으로 단위를 표현하는 인터페이스를 살펴보자.
interface Unit<T : Measure<T>> {
val symbol: String
val name: String
fun convert(value: BigDecimal, toUnit: Unit<T>): BigDecimal
fun create(value: BigDecimal): T
}Unit 인터페이스는 단위의 기호(symbol)와 이름(name)을 가지며, 단위 간 변환(convert)과 새로운 측도 생성(create) 기능을 제공한다. 예를 들어 킬로그램(kg)에서 파운드(lb)로 변환하거나, 5kg의 새로운 무게 객체를 생성할 수 있다.
마지막으로, 특정 종류의 측도에 사용할 수 있는 모든 단위들의 집합을 관리하는 시스템 인터페이스를 정의한다.
interface UnitSystem<T : Measure<T>> {
val baseUnit: MeasurementUnit<T>
val availableUnits: Set<MeasurementUnit<T>>
fun getUnitBySymbol(symbol: String): MeasurementUnit<T>?
fun getUnitByName(name: String): MeasurementUnit<T>?
}UnitSystem은 모든 변환의 기준이 되는 기본 단위(baseUnit)와 사용 가능한 모든 단위들(availableUnits)을 관리한다. 또한 기호나 이름으로 단위를 찾는 메서드도 제공한다.
위에서 정의한 인터페이스를 기반으로 추상 클래스를 구현해보자. 추상 클래스는 인터페이스의 공통 기능을 구현하여 중복 코드를 줄이고, 향후 구현할 구체적인 측도 클래스에서 필요한 기능만 구현할 수 있도록 한다.
abstract class AbstractMeasure<T : Measure<T>>(
override val value: BigDecimal,
override val unit: MeasurementUnit<T>
) : Measure<T> {
override fun convertTo(targetUnit: MeasurementUnit<T>): T {
if (unit == targetUnit) {
@Suppress("UNCHECKED_CAST")
return this as T
}
val convertedValue = unit.convert(value, targetUnit)
return targetUnit.create(convertedValue)
}
override fun compareTo(other: T): Int {
val baseValue = unit.convert(value, getUnitSystem().baseUnit)
val otherBaseValue = other.unit.convert(other.value, getUnitSystem().baseUnit)
return baseValue.compareTo(otherBaseValue)
}
// 다른 연산 메서드들...
abstract fun getUnitSystem(): UnitSystem<T>
}AbstractMeasure 클래스는 convertTo 메서드를 구현하여 다른 단위로 변환할 수 있게 하고, compareTo 메서드를 구현하여 서로 다른 단위의 측도도 비교할 수 있게 한다. 예를 들어 kg과 lb 단위의 무게를 비교할 수 있다.
수량
이제 측도의 값과 단위에 대한 기본 인터페이스를 정의했으니, 이를 활용하여 실제로 수량(Quantity)을 어떻게 표현할 수 있는지 알아볼 것이다.
측도 모델에 기반한 수량 모델은 값과 단위의 개념을 기반으로, 실제 세계의 다양한 측정값을 프로그래밍적으로 표현할 수 있게 해준다. 보통 이러한 수량 모델은 변환에 있어 공식이 정해져 있는 물리적 수량(개수, 무게, 길이, 부피 등)에 사용된다.
수량을 구현하기 위해 Measure 인터페이스를 구현하는 추상 클래스인 Quantity를 먼저 살펴보자. 이 클래스는 모든 종류의 물리적 수량(무게, 길이, 부피 등)의 공통 기능을 제공한다.
abstract class Quantity<T : Measure<T>>(
override val value: BigDecimal,
override val unit: Unit<T>
) : AbstractMeasure<T>(value, unit) {
// 포맷팅을 위한 메서드
fun format(precision: Int = 2): String {
val roundedValue = value.setScale(precision, RoundingMode.HALF_UP)
return "$roundedValue ${unit.symbol}"
}
// toString 재정의
override fun toString(): String = "${value} ${unit.symbol}"
// 동등성 비교
override fun equals(other: Any?): Boolean {
if (this === other) return true
if (other !is Measure<*>) return false
@Suppress("UNCHECKED_CAST")
other as T
return try {
compareTo(other) == 0
} catch (e: ClassCastException) {
false
}
}
// 해시코드 생성
override fun hashCode(): Int {
val baseValue = unit.convert(value, getUnitSystem().baseUnit)
return baseValue.hashCode()
}
}이제 이 추상 클래스를 바탕으로 구체적인 수량 타입들을 구현할 수 있다. 여기서는 무게(Weight)를 예로 들어보자.
class Weight private constructor(
value: BigDecimal,
unit: WeightUnit
) : Quantity<Weight>(value, unit) {
companion object {
// 팩토리 메서드: 기본 생성
fun of(value: BigDecimal, unit: WeightUnit): Weight = Weight(value, unit)
fun of(value: Double, unit: WeightUnit): Weight = of(BigDecimal.valueOf(value), unit)
fun of(value: Int, unit: WeightUnit): Weight = of(BigDecimal.valueOf(value.toLong()), unit)
// 편의 메서드: 특정 단위로 생성
fun kilograms(value: Double): Weight = of(value, WeightSystem.KILOGRAM)
fun grams(value: Double): Weight = of(value, WeightSystem.GRAM)
fun pounds(value: Double): Weight = of(value, WeightSystem.POUND)
fun ounces(value: Double): Weight = of(value, WeightSystem.OUNCE)
}
override fun getUnitSystem(): UnitSystem<Weight> = WeightSystem
}앞서 정의한 Quantity 클래스를 상속받아 Weight 클래스를 구현했다. 이후 편의를 위해 팩토리 메서드를 구현해 다양한 단위로 무게를 생성할 수 있도록 했다. 예를 들어 Weight.kilograms(5.0)은 5kg의 무게 객체를 생성한다.
이어서 무게 단위를 정의하는 WeightUnit 클래스를 구현해보자.
class WeightUnit(
override val symbol: String,
override val name: String,
private val conversionFactor: BigDecimal // 기본 단위(kg)에 대한 변환 계수
) : Unit<Weight> {
override fun convert(value: BigDecimal, toUnit: Unit<Weight>): BigDecimal {
return value.multiply(conversionFactor).divide(toUnit.conversionFactor)
}
override fun create(value: BigDecimal): Weight {
return Weight(value, this)
}
}여기서 conversionFactor는 해당 단위를 기본 단위(킬로그램)로 변환할 때 곱하는 계수이다. 예를 들어 그램은 킬로그램의 1/1000이므로, 그램의 conversionFactor는 0.001이 된다.
마지막으로 무게 단위계를 구현해보자.
object WeightSystem : UnitSystem<Weight> {
val KILOGRAM = WeightUnit("kg", "Kilogram", BigDecimal.ONE)
val GRAM = WeightUnit("g", "Gram", BigDecimal(0.001))
val MILLIGRAM = WeightUnit("mg", "Milligram", BigDecimal(0.000001))
val TON = WeightUnit("t", "Ton", BigDecimal(1000))
val POUND = WeightUnit("lb", "Pound", BigDecimal(0.45359237))
val OUNCE = WeightUnit("oz", "OUNCE", BigDecimal(0.028349523125))
override val baseUnit: Unit<Weight> = KILOGRAM
override val availableUnits: Set<Unit<Weight>> = setOf(KILOGRAM, GRAM, POUND, OUNCE)
override fun getUnitBySymbol(symbol: String): Unit<Weight>? {
return availableUnits.find { it.symbol == symbol }
}
override fun getUnitByName(name: String): Unit<Weight>? {
return availableUnits.find { it.name == name }
}
}WeightSystem은 싱글톤 객체로 구현해서 애플리케이션 전체에서 단 하나의 인스턴스만 존재하도록 만들었다. 이를 통해 단위 정의의 일관성을 보장하고 메모리 사용을 최적화할 수 있다. 이제 이를 사용한 예제 코드를 살펴보자.
// 무게 생성
val weight1 = Weight.kilograms(75.5)
val weight2 = Weight.pounds(150.0)
// 단위 변환
val weight2InKg = weight2.convertTo(WeightSystem.KILOGRAM)
println("150 pounds = ${weight2InKg}") // "150 pounds = 68.0388555 kg"
// 무게 덧셈
val totalWeight = weight1.add(weight2)
println("Total weight: $totalWeight") // "Total weight: 143.5388555 kg"
// 무게 비교
val isHeavier = weight1 > weight2
println("Is 75.5 kg heavier than 150 pounds? $isHeavier") // true이와 같은 방식으로 무게 외에도 다양한 측도를 구현할 수 있다. 예를 들어 거리를 표현하는 Distance 클래스, 부피를 표현하는 Volume 클래스 등을 구현할 수 있다. 각 클래스는 Measure 인터페이스를 구현하고, 단위와 단위계도 각각 정의하면 된다.
각 수량 타입은 고유한 단위 시스템과 단위 간 변환 규칙을 가지지만, 기본적인 구조와 연산 방식은 동일하게 유지된다. 이는 객체지향 설계의 다형성과 상속을 잘 활용한 예시이다.
화폐
앞서 구현한 수량 모델으로 해결할 수 없는 단위도 있다. 그 중 하나가 화폐이다. 화폐는 단순히 수량과 단위의 조합인 동시에, 환율이라는 특수한 변환 관계를 가지고 있다. 또한 비즈니스 애플리케이션에서 가장 많이 사용되는 측도 중 하나이다. 이번에는 앞서 구현한 측도 시스템을 바탕으로 화폐를 어떻게 모델링할 수 있는지 살펴보자.
먼저 화폐는 일반적인 물리적 수량과 달리 몇 가지 고유한 특성을 가지고 있다. ISO 표준 코드가 존재하고, 환율이 있으므로 변환이 고정되어 있지 않다. 이를 고려하여 화폐 모델을 구현해보자. 먼저 화폐를 표현하는 Money 클래스를 정의해보자.
class Money private constructor(
value: BigDecimal,
unit: CurrencyUnit
) : AbstractMeasure<Money>(value, unit) {
companion object {
// 팩토리 메서드
fun of(value: BigDecimal, currency: CurrencyUnit): Money = Money(value, currency)
fun of(value: Double, currency: CurrencyUnit): Money = of(BigDecimal.valueOf(value), currency)
fun of(value: Int, currency: CurrencyUnit): Money = of(BigDecimal.valueOf(value.toLong()), currency)
// 주요 통화별 편의 메서드
fun usd(value: Double): Money = of(value, CurrencySystem.USD)
fun eur(value: Double): Money = of(value, CurrencySystem.EUR)
fun jpy(value: Double): Money = of(value, CurrencySystem.JPY)
fun krw(value: Double): Money = of(value, CurrencySystem.KRW)
}
// 통화 단위에 더 직관적으로 접근하기 위한 속성
val currency: CurrencyUnit
get() = unit as CurrencyUnit
// 화폐 포맷팅
fun format(locale: Locale = Locale.getDefault()): String {
val formatter = NumberFormat.getCurrencyInstance(locale).apply {
currency = java.util.Currency.getInstance(this@Money.currency.code)
}
return formatter.format(value)
}
// 간단한 포맷팅
fun formatSimple(): String = "${currency.symbol}$value"
override fun getUnitSystem(): UnitSystem<Money> = CurrencySystem
// 화폐 연산에 특화된 메서드들
fun percentage(percent: Double): Money {
val factor = BigDecimal.valueOf(percent).divide(BigDecimal("100"), 10, RoundingMode.HALF_UP)
return multiply(factor)
}
fun addPercentage(percent: Double): Money {
val factor = BigDecimal.ONE.add(BigDecimal.valueOf(percent).divide(BigDecimal("100"), 10, RoundingMode.HALF_UP))
return multiply(factor)
}
}Money 클래스를 구현하며 기본적인 측도 기능을 상속받으면서 화폐에 특화된 기능을 추가했다. 먼저 currency 필드를 통해 확장된 Unit 타입인 CurrencyUnit에 접근할 수 있도록 했다. 그리고 format 메서드를 통해 지역화된 화폐 포맷팅을 지원하며, 세금이나 할인율과 같은 퍼센트 기반 연산을 쉽게 수행할 수 있는 메서드를 제공했다.
다음으로 화폐 단위를 정의하는 CurrencyUnit 클래스를 구현해보자.
class CurrencyUnit(
override val symbol: String,
override val name: String,
val code: String, // ISO 통화 코드 (예: USD, EUR)
var exchangeRate: BigDecimal // 기준 통화(예: USD)에 대한 환율, 변할 수 있음
) : Unit<Money> {
override fun convert(value: BigDecimal, toUnit: Unit<Money>): BigDecimal {
toUnit as CurrencyUnit
// 기본 통화로 변환 후 대상 통화로 변환
val valueInBaseUnit = value.divide(exchangeRate, 10, RoundingMode.HALF_UP)
return valueInBaseUnit.multiply(toUnit.exchangeRate)
}
override fun create(value: BigDecimal): Money = Money.of(value, this)
}CurrencyUnit은 일반적인 단위 정보(기호, 이름) 외에도 ISO 통화 코드와 환율을 추가로 저장한다. 그리고 convert 메서드에서는 일반적인 물리적 단위와 달리, 직접적인 변환이 아닌 USD와 같은 기준 통화를 경유한 변환을 수행한다. 이는 금융 시스템에서 일반적으로 사용되는 방식으로, 모든 통화 쌍에 대한 환율을 개별적으로 관리하지 않고, 기준 통화에 대한 환율만 관리하는 방식이다.
마지막으로 통화 단위들을 관리하는 CurrencySystem을 구현해보자.
object CurrencySystem : AbstractUnitSystem<Money>() {
// 주요 통화 정의
val USD = CurrencyUnit("$", "US Dollar", "USD", BigDecimal.ONE)
val EUR = CurrencyUnit("€", "Euro", "EUR", BigDecimal("1.09"))
val GBP = CurrencyUnit("£", "British Pound", "GBP", BigDecimal("1.27"))
val JPY = CurrencyUnit("¥", "Japanese Yen", "JPY", BigDecimal("0.0067"))
val KRW = CurrencyUnit("₩", "Korean Won", "KRW", BigDecimal("0.00074"))
override val baseUnit: Unit<Money> = USD // 기준 통화: USD
override val availableUnits: Set<Unit<Money>> = setOf(
USD, EUR, GBP, JPY, KRW
)
// 통화 코드로 통화 단위 찾기
fun getUnitByCode(code: String): CurrencyUnit? {
return availableUnits.find {
(it as CurrencyUnit).code.equals(code, ignoreCase = true)
} as CurrencyUnit?
}
// 환율 업데이트
fun updateExchangeRate(currencyCode: String, newRate: BigDecimal) {
val currency = getUnitByCode(currencyCode) ?:
throw IllegalArgumentException("Unknown currency code: $currencyCode")
currency.exchangeRate = newRate
}
}CurrencySystem은 주요 통화들을 정의하고, 기준 통화와 사용 가능한 통화 단위들을 관리한다. 또한 통화 코드로 단위를 찾는 메서드와 환율을 업데이트하는 메서드를 제공한다. 여기서는 단순화를 위해 환율 정보를 하드코딩된 값으로 사용했지만, 실제 애플리케이션에서는 외부 API를 통해 실시간으로 가져와서 최신 환율을 반영해야 한다. 예를 들어, Open Exchange Rates와 같은 서비스를 사용하여 환율 정보를 가져올 수 있다. 여기서 환율 정보를 가져오는 구현은 생략한다.
이제 Money 클래스를 사용하여 화폐를 표현하고, 다양한 연산을 수행할 수 있다. 예를 들어, 다음과 같이 화폐 객체를 생성하고 연산을 수행할 수 있다.
// 화폐 생성
val usd100 = Money.usd(100.0)
val eur50 = Money.eur(50.0)
// 간단한 포맷팅
println("USD amount: ${usd100.formatSimple()}") // "USD amount: $100.0"
// 지역화된 포맷팅
println("EUR amount in US format: ${eur50.format(Locale.US)}") // "EUR amount in US format: €50.00"
println("EUR amount in German format: ${eur50.format(Locale.GERMANY)}") // "EUR amount in German format: 50,00 €"
// 통화 변환
val eurToUsd = eur50.convertTo(CurrencySystem.USD)
println("50 EUR = ${eurToUsd.formatSimple()}") // "50 EUR = $54.5"
// 화폐 연산
val total = usd100.add(eur50.convertTo(CurrencySystem.USD))
println("Total: ${total.formatSimple()}") // "Total: $154.5"
// 퍼센트 계산 (세금, 할인 등)
val tax = usd100.percentage(8.0) // 8% 세금
println("8% tax on $100: ${tax.formatSimple()}") // "8% tax on $100: $8.0"
val withTax = usd100.addPercentage(8.0) // 세금 포함 금액
println("$100 with 8% tax: ${withTax.formatSimple()}") // "$100 with 8% tax: $108.0"이런 방식을 통해 수량 모델과는 다르게, 화폐라는 특수한 모델에 대해서도 대응이 가능하다. 보통 특수한 측도는 다음과 같은 특성을 가진다.
- 비선형 변환: 단순한 곱셈/나눗셈이 아닌 복잡한 변환 공식이 필요하다.
- 특별한 의미론: 덧셈, 뺄셈 등 연산의 의미가 일반 측도와 다를 수 있다.
- 도메인 특화 로직: 각 도메인에 특화된 추가 기능이 필요하다.
- 문화적/지역적 차이: 같은 측도도 문화권이나 지역에 따라 다른 표현 방식을 가질 수 있다.
화폐 외에도 데이터 크기(KB, MB, GB 등), 시간, 온도, 주파수 등은 일반적인 물리적 수량과는 다른 변환 관계나 연산을 가지므로, 수량 모델이 아닌 별도의 모델이 필요하다.
수학적 측도
앞서 다룬 일상적인 단위 외에 수학적 측도는 물리적 수량과는 다른 개념으로, 비율(Ratio)이나 각도(Angle), 지수(Exponent) 등과 같은 수학적 개념을 표현하는 데 사용된다.
수학적 측도는 기존 측도를 이용하여 연산 후 결과를 표현하는 데 사용된다. 예를 들어, 비율은 두 수량 간의 관계를 나타내며, 각도는 회전이나 기울기를 나타낸다. 이러한 측도는 일반적으로 물리적 수량과는 다른 연산 규칙을 가지므로, 별도의 모델로 구현하는 것이 좋다.
먼저 비율을 살펴보자. 비율은 두 수량 간의 관계를 나타내는 값으로, 일반적으로 분수 형태로 표현된다. 이를 표현할 수 있는 Ratio를 구현해보자.
class RatioUnit(
override val symbol: String,
override val name: String,
val conversionFactor: BigDecimal // 십진수(decimal) 기준 변환 계수
) : Unit<Ratio> {
override fun convert(value: BigDecimal, toUnit: Unit<Ratio>): BigDecimal {
toUnit as RatioUnit
// 기본 단위(십진수)로 변환 후 목표 단위로 변환
val valueInDecimal = value.multiply(conversionFactor)
return valueInDecimal.divide(toUnit.conversionFactor, 10, RoundingMode.HALF_UP)
}
override fun create(value: BigDecimal): Ratio = Ratio.of(value, this)
}
class Ratio private constructor(
value: BigDecimal,
unit: RatioUnit
) : AbstractMeasure<Ratio>(value, unit) {
companion object {
fun of(value: BigDecimal, unit: RatioUnit): Ratio = Ratio(value, unit)
fun of(value: Double, unit: RatioUnit): Ratio = of(BigDecimal.valueOf(value), unit)
// 편의 메서드
fun decimal(value: Double): Ratio = of(value, RatioSystem.DECIMAL)
fun percentage(value: Double): Ratio = of(value, RatioSystem.PERCENTAGE)
fun permille(value: Double): Ratio = of(value, RatioSystem.PERMILLE)
fun fraction(numerator: Int, denominator: Int): Ratio {
val value = BigDecimal.valueOf(numerator.toLong())
.divide(BigDecimal.valueOf(denominator.toLong()), 10, RoundingMode.HALF_UP)
return decimal(value.toDouble())
}
}
override fun getUnitSystem(): UnitSystem<Ratio> = RatioSystem
// 편의 변환 메서드
fun toPercentage(): Ratio = convertTo(RatioSystem.PERCENTAGE)
fun toDecimal(): Ratio = convertTo(RatioSystem.DECIMAL)
// 두 측도의 비율 계산을 위한 정적 메서드
companion object {
fun <T : Measure<T>> between(value1: T, value2: T): Ratio {
if (value1.unit != value2.unit) {
throw IllegalArgumentException("Cannot compute ratio between different units without conversion")
}
val ratio = value1.value.divide(value2.value, 10, RoundingMode.HALF_UP)
return decimal(ratio.toDouble())
}
// 측도의 변화율 계산
fun <T : Measure<T>> changeRate(oldValue: T, newValue: T): Ratio {
val convertedNew = if (oldValue.unit != newValue.unit) {
newValue.convertTo(oldValue.unit as Unit<T>)
} else {
newValue
}
val change = convertedNew.value.subtract(oldValue.value)
val rate = change.divide(oldValue.value, 10, RoundingMode.HALF_UP)
return decimal(rate.toDouble())
}
}
// 비율 연산
fun add(other: Ratio): Ratio {
val convertedOther = other.convertTo(unit as RatioUnit)
val sum = value.add(convertedOther.value)
return Ratio.of(sum, unit as RatioUnit)
}
operator fun plus(other: Ratio): Ratio = add(other)
// 측도에 비율 적용
fun <T : Measure<T>> applyTo(measure: T): T {
val decimalRatio = this.convertTo(RatioSystem.DECIMAL)
return measure.multiply(decimalRatio.value)
}
// 증가율 적용 (1 + rate)
fun <T : Measure<T>> increase(measure: T): T {
val decimalRatio = this.convertTo(RatioSystem.DECIMAL)
val factor = BigDecimal.ONE.add(decimalRatio.value)
return measure.multiply(factor)
}
}
object RatioSystem : AbstractUnitSystem<Ratio>() {
val DECIMAL = RatioUnit("", "decimal", BigDecimal.ONE)
val PERCENTAGE = RatioUnit("%", "percentage", BigDecimal("0.01"))
val PERMILLE = RatioUnit("‰", "permille", BigDecimal("0.001"))
val BASIS_POINT = RatioUnit("bp", "basis point", BigDecimal("0.0001"))
override val baseUnit: Unit<Ratio> = DECIMAL
override val availableUnits: Set<Unit<Ratio>> = setOf(
DECIMAL, PERCENTAGE, PERMILLE, BASIS_POINT
)
}위와 같이 Ratio를 구현하면, 두 수량 간의 비율을 쉽게 계산할 수 있다. 예를 들어, 두 무게 간의 비율을 계산할 때는 다음과 같이 사용할 수 있다.
val weight1 = Weight.kilograms(50.0)
val weight2 = Weight.kilograms(25.0)
val ratio = Ratio.between(weight1, weight2)
println("Ratio of weight1 to weight2: ${ratio}") // "Ratio of weight1 to weight2: 2.0"혹은 이자와 같은 금융 비율을 계산할 때도 사용할 수 있다.
val interestRate = Ratio.percentage(5.0) // 5%
val principal = Money.usd(1000.0)
val interest = interestRate.applyTo(principal)
println("Interest on $1000 at 5%: ${interest.formatSimple()}") // "Interest on $1000 at 5%: $50.0"이렇게 수학적 측도를 구현하면, 다양한 수량 간의 관계를 표현하고 계산할 수 있다. 외에도 다양한 수학적 측도를 구현할 수 있으며, 각 측도에 맞는 단위와 변환 규칙을 정의하면 된다.
복합 측도와 파생 측도
앞서 살펴본 기본 측도(수량)와 특수 측도(화폐 등)를 넘어, 현실 세계에서는 여러 측도가 결합되거나 파생되는 경우가 많다. 이러한 복합 측도와 파생 측도를 모델링하는 방법을 알아보자.
복합 측도
복합 측도는 두 개 이상의 기본 측도가 결합된 형태를 말한다. 예를 들어 속도는 거리와 시간의 비율(km/h)로, 밀도는 질량과 부피의 비율(kg/m³)로 표현된다.
복합 측도를 모델링할 때는 기존 측도를 조합하여 새로운 측도를 생성하는 방식으로 구현할 수 있다. 예를 들어 속도를 표현하는 Velocity를 구현해보자.
먼저 속도에 대한 단위를 정의하는 VelocityUnit 클래스를 구현한다. 이 클래스는 거리 단위와 시간 단위를 조합하여 속도를 표현한다.
class VelocityUnit(
override val symbol: String,
override val name: String,
// 거리 단위와 시간 단위를 조합
val distanceUnit: Unit<Distance>,
val timeUnit: Unit<Time>
) : AbstractUnit<Velocity>() {
override fun convert(value: BigDecimal, toUnit: Unit<Velocity>): BigDecimal {
toUnit as VelocityUnit
// 거리 단위 변환 계수
val distanceFactor = distanceUnit.convert(
BigDecimal.ONE,
toUnit.distanceUnit
)
// 시간 단위 변환 계수
val timeFactor = timeUnit.convert(
BigDecimal.ONE,
toUnit.timeUnit
)
// 속도 변환: (거리 변환 / 시간 변환) * 원래 값
return value.multiply(distanceFactor).divide(timeFactor, 10, RoundingMode.HALF_UP)
}
override fun create(value: BigDecimal): Velocity = Velocity.of(value, this)
}위 코드를 보면 VelocityUnit 클래스는 거리 단위와 시간 단위를 조합하여 속도를 표현한다. convert 메서드는 거리 단위와 시간 단위를 각각 변환한 후, 속도 변환을 수행한다. 예를 들어 60km/h를 m/s로 변환할 때, 거리 단위는 km에서 m로, 시간 단위는 h에서 s로 변환하여 최종 속도를 계산한다.
다음으로 속도를 표현하는 Velocity 클래스를 구현해보자.
class Velocity private constructor(
value: BigDecimal,
unit: VelocityUnit
) : AbstractMeasure<Velocity>(value, unit) {
companion object {
fun of(value: BigDecimal, unit: VelocityUnit): Velocity = Velocity(value, unit)
fun of(value: Double, unit: VelocityUnit): Velocity = of(BigDecimal.valueOf(value), unit)
// 편의 메서드
fun metersPerSecond(value: Double): Velocity = of(value, VelocitySystem.METERS_PER_SECOND)
fun kilometersPerHour(value: Double): Velocity = of(value, VelocitySystem.KILOMETERS_PER_HOUR)
fun milesPerHour(value: Double): Velocity = of(value, VelocitySystem.MILES_PER_HOUR)
}
override fun getUnitSystem(): UnitSystem<Velocity> = VelocitySystem
// 거리 계산 (속도 × 시간)
fun multiply(time: Time): Distance {
val velocityUnit = unit as VelocityUnit
val convertedTime = time.convertTo(velocityUnit.timeUnit)
val distanceValue = value.multiply(convertedTime.value)
return Distance.of(distanceValue, velocityUnit.distanceUnit as DistanceUnit)
}
// 시간 계산 (거리 ÷ 속도)
fun timeToTravel(distance: Distance): Time {
val velocityUnit = unit as VelocityUnit
val convertedDistance = distance.convertTo(velocityUnit.distanceUnit as DistanceUnit)
val timeValue = convertedDistance.value.divide(value, 10, RoundingMode.HALF_UP)
return Time.of(timeValue, velocityUnit.timeUnit)
}
}여기서 주목할 점은 multiply 메서드와 timeToTravel 메서드이다. multiply 메서드는 속도와 시간을 곱하여 거리를 계산하고, timeToTravel 메서드는 거리를 속도로 나누어 시간을 계산한다. 이처럼 복합 측도는 기본 측도를 조합하여 새로운 기능을 제공할 수 있다.
마지막으로 속도 단위계를 정의하는 VelocitySystem을 구현해보자.
object VelocitySystem : AbstractUnitSystem<Velocity>() {
val METERS_PER_SECOND = VelocityUnit("m/s", "meters per second",
DistanceSystem.METER, TimeSystem.SECOND)
val KILOMETERS_PER_HOUR = VelocityUnit("km/h", "kilometers per hour",
DistanceSystem.KILOMETER, TimeSystem.HOUR)
val MILES_PER_HOUR = VelocityUnit("mph", "miles per hour",
DistanceSystem.MILE, TimeSystem.HOUR)
val FEET_PER_SECOND = VelocityUnit("ft/s", "feet per second",
DistanceSystem.FOOT, TimeSystem.SECOND)
override val baseUnit: Unit<Velocity> = METERS_PER_SECOND
override val availableUnits: Set<Unit<Velocity>> = setOf(
METERS_PER_SECOND, KILOMETERS_PER_HOUR, MILES_PER_HOUR, FEET_PER_SECOND
)
// 속도 생성 메서드
fun from(distance: Distance, time: Time): Velocity {
// 기본 단위로 변환
val baseDistance = distance.convertTo(DistanceSystem.METER)
val baseTime = time.convertTo(TimeSystem.SECOND)
// 속도 계산
val velocityValue = baseDistance.value.divide(baseTime.value, 10, RoundingMode.HALF_UP)
return Velocity.of(velocityValue, METERS_PER_SECOND)
}
}위와 같이 여러 단위가 정의된 복합 측도도 기본 측도 모델로 구현할 수 있다.
파생 측도
이어서 파생 측도는 기본 측도를 기반으로 만들 수 있는 새로운 측도다. 대표적인 예로 길이를 곱하여 면적을 구하거나, 길이와 면적을 곱하여 부피를 구하는 경우가 있다. 이런 경우 다음과 같이 코드를 작성할 수 있다.
class Distance private constructor(
value: BigDecimal,
unit: DistanceUnit
) : AbstractMeasure<Distance>(value, unit) {
// 기존 메서드들...
// 두 길이를 곱해 직사각형 면적 계산
fun area(other: Distance): Area {
// 같은 단위로 변환
val convertedOther = other.convertTo(unit as DistanceUnit)
// 면적 계산
val areaValue = value.multiply(convertedOther.value)
// 길이 단위에 맞는 면적 단위 생성
val areaUnit = AreaUnit.fromDistanceUnit(unit as DistanceUnit)
return Area.of(areaValue, areaUnit)
}
// 정사각형 면적
fun square(): Area {
return this.multiply(this)
}
}위와 같이 area 메서드를 통해 두 길이를 곱하여 면적을 계산할 수 있다. 이때 면적 단위는 길이 단위를 기반으로 생성할 수 있다. 예를 들어 미터(m) 단위의 길이를 곱하면 제곱미터(m²) 단위의 면적이 된다. 이를 위해 AreaUnit에서 fromDistanceUnit 메서드를 구현하여 길이 단위를 기반으로 면적 단위를 생성할 수 있도록 만들어야 한다.
class AreaUnit(
override val symbol: String,
override val name: String,
val conversionFactor: BigDecimal // 기본 단위(m²)에 대한 변환 계수
) : Unit<Area> {
companion object {
// 길이 단위로부터 면적 단위 생성
fun fromDistanceUnit(unit: DistanceUnit): AreaUnit {
val symbol = "${unit.symbol}²"
val name = "square ${unit.name}"
// 길이 변환 계수의 제곱이 면적 변환 계수가 됨
val conversionFactor = unit.conversionFactor.pow(2)
return AreaUnit(symbol, name, conversionFactor)
}
}
override fun convert(value: BigDecimal, toUnit: Unit<Area>): BigDecimal {
// ... 면적 단위 변환 로직
}
override fun create(value: BigDecimal): Area = Area.of(value, this)
}
// Area, AreaSystem 구현 생략이런 방식으로 측도와 측도 간의 관계를 정의하여 파생 측도를 구현할 수 있다. 측도는 독립적으로만 존재하는 것이 아니라, 서로 관계를 맺고 있으며, 이를 통해 복합 측도와 파생 측도를 모델링할 수 있다. 이러한 관계를 잘 정의하면, 다양한 물리적 현상을 프로그래밍적으로 표현할 수 있다.
마치며
지금까지 측도 모델을 통해 어떻게 다양한 물리적 수량을 표현하고, 단위 변환 및 연산을 수행할 수 있는지 살펴보았다. 측도 모델은 객체지향 설계의 원칙을 잘 활용하여, 코드의 재사용성과 유지보수성을 높일 수 있는 강력한 도구이다. 또한 안정성 측면에서도 원시 타입을 사용하는 것보다 훨씬 안전하다.
소프트웨어가 어떤 가치를 제공하냐에 따라 필요한 측도는 다를 수 있다. 따라서 측도 모델을 설계할 때는 도메인에 맞는 측도를 정의하고, 필요한 연산과 변환을 고려하여 설계해야 한다. 또한, 측도 모델은 단순히 수량을 표현하는 것뿐만 아니라, 비즈니스 로직을 구현하는 데에도 큰 도움이 된다.
