필자는 쓸데없지만 재밌는 프로그램을 만들면서 공부하는 것을 좋아한다. 최근에 정신적으로 에너지가 바닥나고 있다는 것을 느껴 작년에 재미로 만들었던 Jazzlang과 같이 정신적 에너지를 채워줄만한 재미를 느끼고 싶었다. 그래서 무언가 할만한 것을 찾던 중 작년 이맘때 쯤 재밌는 유튜브 영상을 봤던 것이 생각났다. 영상에서는 CLI 환경에서 큐브를 회전시키는 프로그램을 처음부터 끝까지 조용히 코딩하는 것을 보여준다.

필자는 이 아이디어가 굉장히 참신하다 생각했다. 마침 무언가를 만들고 싶었던 차에 큐브가 됐다면 CLI 환경에서 다른 물체도 3D 렌더링 할 수 있지 않을까?라는 생각을 하게되었고 실제로 구현했다. 이 글의 결과물은 GitHub 저장소와 Chromatic에서 볼 수 있다.
어떻게 ASCII를 3D처럼 보이게 할까?
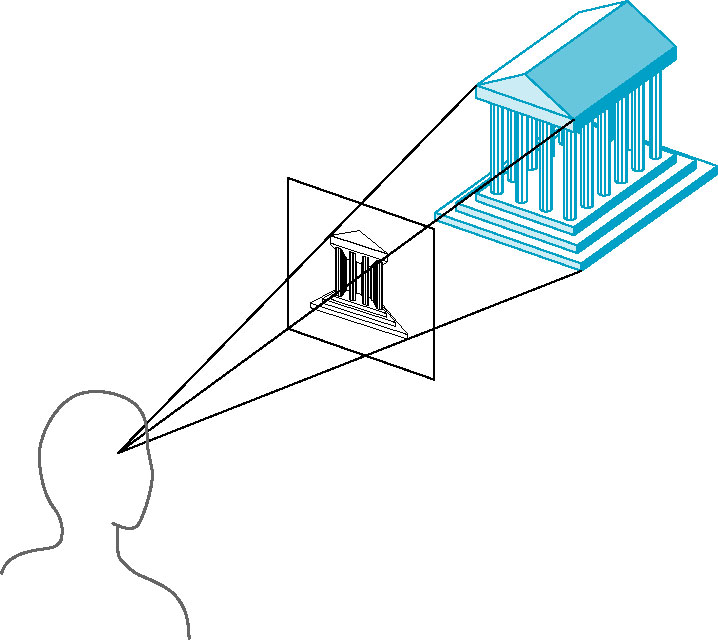
3D 렌더링은 빛과 그림자, 최적화, 쉐이더, 충돌 처리, 물리 계산 등 굉장히 난이도가 높은 기술이 포함된다. 하지만 우리는 단순히 3D 물체를 화면에 그리기만 할 것이기 때문에 몇 가지 기본적인 기술만 알면 된다. 우리는 화면에 나오는 물체를 왜 삼차원 공간으로 인식을 할까? 답은 간단하다. 스크린을 통해 원근감을 표현했기 때문이다. 사람이 원근감을 느끼도록 만드는 방법은 다양하지만 일반적인 CLI 환경에서 쓸 수 있는 것은 선1과 명암 뿐이다.

선을 이용하여 원근감을 표현하는 방법은 간단하다. 멀리있는 것은 결국 한 점으로 모인다는 사실을 이용할 수 있다. 이를 미술 용어로 소실점이라 부른다. 소실점은 여러 개가 있을 수 있다.
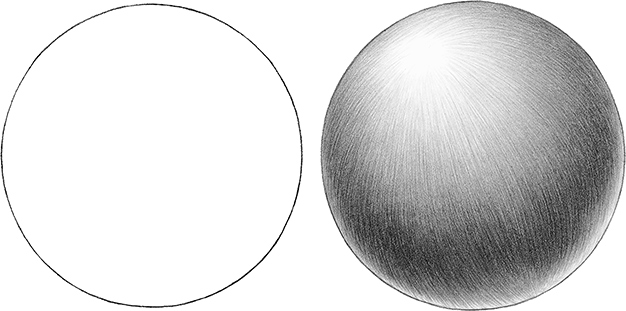
명암을 포함한 원근감을 표현하는 방법은 더욱 간단하다. 빛이 있는 곳은 밝게, 빛이 없는 곳은 어둡게 표현하면 된다. 이를 통해 물체의 입체감을 표현할 수 있다.
그런데 ASCII 만으로 원금감, 입체감을 표현할 수 있을까? 우선 결론부터 이야기하자면 ASCII를 이용한다는 것은 사실 조금 큰 픽셀이라 생각하면 된다. 다음 이미지를 보자.

좌측은 원본 이미지 우측은 Pixelate 이펙트를 입힌 이미지다. ASCII를 사용한다는 것은 단지 글자를 이용하여 우측 이미지 처럼 만드는 것과 크게 다르지 않다. 이를 이용한 작품도 존재한다.

위 이미지를 보면 텍스트만으로 충분히 이미지를 표현할 수 있다는 것을 알 수 있다. 그리고 빛이 보고있는 방향에서 나온다 가정했을 때 가까이 있을 수록 짙은 텍스트 멀리 있을 수록 옅은 텍스트로 나타냈기에 원근감과 명암마저도 표현할 수 있다.
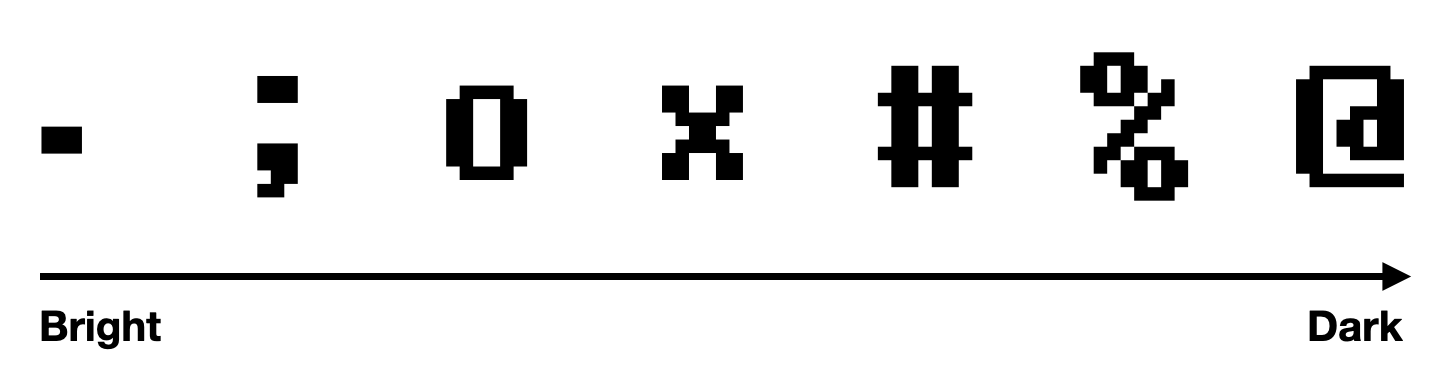
참고로 간격이 일정해야 하므로 반드시 고정폭 글꼴을 사용해야 한다. 앞서 소개했던 유튜브 영상에서 나오는 큐브처럼 명암을 표현하면 다음과 같다.
위 예제는 필자가 유튜브 영상에 나온 프로그램을 직접 웹에서 실행 가능하도록 구현한 것이다. 빛에 기반한 명암 처리는 아니지만 각 면의 명암이 다르기에 입체감을 느낄 수 있다. 이제 이를 구현하기 위해 필요한 지식을 알아보자.
3D 좌표를 2D 좌표로
우리가 표현하고자 하는 물체는 3D 공간에 존재하지만 모니터 스크린은 2D 공간이다. 따라서 이를 표현하기 위해서는 값으로 정의된 3D 공간을 모니터 스크린인 2D 공간에 보이도록 변환시킬 필요가 있다. 이런 변환하는 과정을 렌더링 파이프라인이라고 한다.
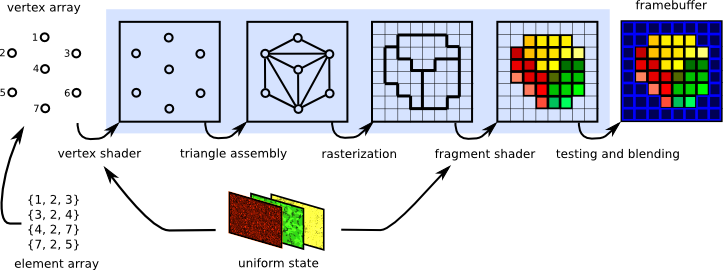
이 글에서는 오로지 ASCII를 이용하여 3D 물체를 표현하는 것이 목표이므로 렌더링 파이프라인의 일부만 구현할 것이다. 그렇기 때문에 전체를 자세히 설명하지는 않고 필요한 부분만 설명할 것이다. 렌더링 파이프라인은 크게 보면 세 과정으로 이루어진다.
- 버텍스 처리 (Vertex processing)
- 래스터화 (Rasterization)
- 프래그먼트 처리 (Fragment processing)
각 과정을 하나씩 살펴보자.
버텍스 처리
3D 공간을 표현하기 위해서는 3D 공간 좌표가 필요하다. 3D 공간 좌표는 데카르트 좌표계를 사용하여 좌표를 3개의 축 (x, y, z)와 같이 표현한다. 어려운 용어처럼 느껴지지만 그냥 3개의 값으로 좌표를 표현한다고 생각하면 된다.
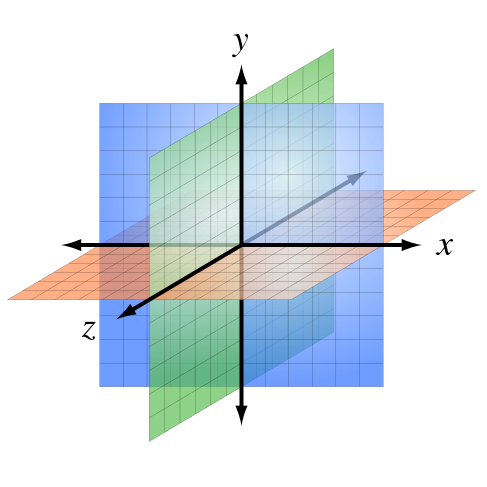
이렇게 표현된 좌표를 버텍스Vertex라고 부르며 3D 공간에 위치한 '정점'을 의미한다. 버텍스 하나로는 물체를 표현할 수 없으므로 버텍스를 모아 물체를 표현한다. 이때 물체를 표현하는 최소 단위를 폴리곤Polygon이라고 부른다. 보통 폴리곤은 특수한 경우2를 제외하면 3개의 버텍스로 이루어진 삼각형으로 표현한다. 하필 삼각형인 이유는 면을 구성하기 위해 필요한 최소 단위가 삼각형이며 효율적이기 때문이다.

이렇게 버텍스와 폴리곤으로 구성된 하나의 물체를 폴리곤 메시Polygon mesh라고 부른다. 보통 개발자는 디자이너가 만들어준 3D 모델 파일을 불러와서 폴리곤 메시를 만든다. 3D 모델 파일에는 버텍스와 폴리곤을 포함한 다양한 정보가 담겨있다. 이 정보를 통해 물체를 표현할 수 있다. 이 과정에서 버텍스를 변형하는 과정을 버텍스 처리Vertex processing라고 부른다.
버텍스 처리 단계에서 버텍스에 대한 여러 처리를 할 수 있지만 보통 변환을 처리하는 것이 가장 기본이다. 여기서 말하는 변환이 3D 공간을 2D 스크린으로 옮기는 핵심이다. 버텍스 처리 과정에서 변환은 보통 세 단계를 거친다.
- 월드 변환 (World transform)
- 뷰 변환 (View transform)
- 투영 변환 (Projection transform)
각 변환은 행렬Matrix을 이용하여 처리한다. 이제 각 변환에 대해 알아보자.
월드 변환
월드 변환은 3D 모델 파일에 담겨있는 버텍스를 월드라고 부르는 3D 공간에 배치하는 것이다. 3D 모델 파일은 자신만의 공간에서 고정된 값을 가지지만 월드에 배치할 위치나 크기, 회전 각도에 따라 새로운 값을 부여해줄 필요가 있다. 모델 좌표를 변경하여 월드에 배치하는 것이기 때문에 모델 변환이라 부르기도 한다.

앞서 설명한 것처럼 좌표 변환은 행렬을 이용하여 처리한다. 이때 변환을 처리하기 위한 행렬은 3차원 좌표를 처리함에도 불구하고 4x4 행렬을 사용한다. 각각 하나씩만 처리한다면 3x3 행렬을 사용해도 문제 없지만 이동, 크기, 회전을 한 번에 처리하기 위해서는 4x4 행렬을 사용해야 한다.3
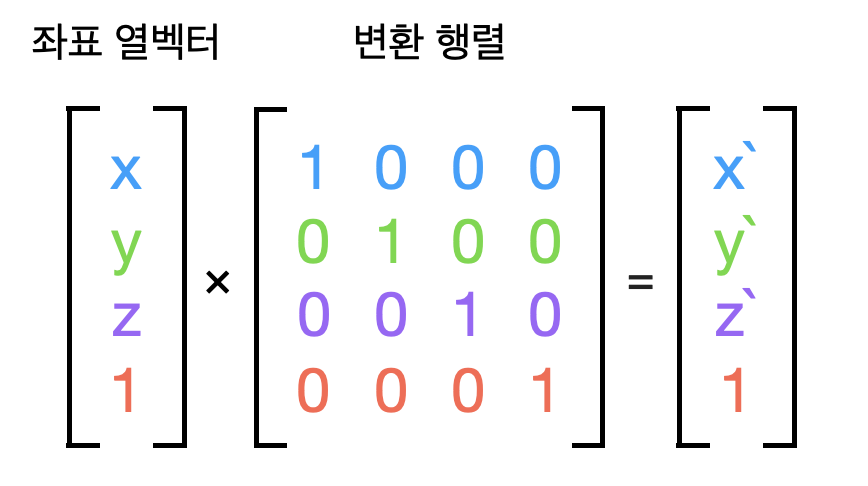
이동, 크기, 회전에 대한 행렬이 존재하지만 지금은 우선 그런 것들이 있다는 것만 이해하고 넘어가자. 요약하자면 버텍스 위치에 대한 열벡터(1×4 행렬)와 각 행렬을 모두 곱하는 것이 월드 변환이다. 월드 변환을 마치고나면 불러온 모델을 월드에 절대적인 좌표로 배치했다고 볼 수 있다.
뷰 변환
월드 변환을 통해 절대적인 좌표로 모델을 월드에 배치했지만 아직 스크린에 표현할 수는 없다. 스크린에 표현하기 위해서는 어느 좌표에서 어느 시점으로 물체를 바라보는지 알아야 한다. 그 좌표와 시점을 포함한 것을 카메라라고 부르며 카메라의 위치에 따라 물체가 보이는 모습이 달라질 수 있다. 따라서 카메라의 위치와 방향을 월드에 배치하고 모델의 좌표를 카메라의 위치를 기준으로 변환해야 한다. 이를 뷰 변환이라 부른다. 혹은 카메라 값에 따라 달라지기 때문에 카메라 변환이라고 부르기도 한다.
카메라를 표현하는 값은 세 가지가 있다.
- 카메라 위치 (Eye)
- 카메라 방향 (Look)
- 카메라 업 벡터 (Up)
카메라 위치는 카메라가 월드에서 어디에 위치하는지를 나타내는 값이다. 카메라 방향은 카메라가 어느 방향을 바라보는지를 나타내는 값이다. 카메라 업 벡터는 카메라가 어느 방향을 위로 할지를 나타내는 값이다. 카메라 업 벡터는 카메라 방향과 수직이어야 한다. 이 세 가지 값은 카메라를 표현하는 좌표계를 구성한다. 이를 카메라 좌표계라고 부른다.
이후에 뷰 변환을 할 때는 카메라 좌표계를 이용하여 카메라를 기준으로 다른 물체의 좌표를 변환하게 된다. 따라서 모든 물체에 카메라에 대한 역행렬을 적용하면 된다. 참고로 뷰 변환을 할 때는 아직 원근감을 표현하지 않는다. 원근감을 표현하기 위해서는 투영 변환이 필요하다.
투영 변환
앞서 설명한 것처럼 원근감을 표현하기 위해서 투영 변환을 해야한다. 투영 변환은 크게 직교 투영과 원근 투영 두 가지로 나뉘지만 직교 투영은 원근감을 표현하지 않는 방��법4이기 때문에 3D 렌더링을 위해선 원근 투영을 사용한다.
원근 투영은 네 가지 속성을 통해 변환을 처리한다.
- 시야각 (Field of view)
- 종횡비 (Aspect ratio)
- 가까운 평면 (Near plane)
- 먼 평면 (Far plane)
시야각은 카메라가 얼마나 넓은 각도로 보이는지를 나타내는 값이다. 종횡비는 화면의 가로 세로 비율을 나타내는 값이다. 가까운 평면과 먼 평면은 카메라가 보이는 화면의 범위를 나타내는 값이다. 이 네 가지 속성을 이용하여 원근 투영을 처리한다.
원근 투영을 처리할 때 위 네 가지 속성을 통해 투영 행렬을 만들 수 있다. 투영 행렬은 4x4 행렬로 구성되며 이 투영 행렬을 이용하여 뷰 변환을 마친 좌표를 2D 공간 좌표로 변환할 수 있다. 투영 행렬은 다음과 같이 구성한다.
이렇게 투영 변환 과정을 거치면 3D 공간 좌표를 2D 공간 좌표로 변환했다고 볼 수 있다. 이제 래스터화를 통해 2D 공간 좌표를 픽셀 좌표로 변환해야 한다.
래스터화
버텍스 처리를 통해 3D 공간 좌표를 2D 공간 좌표로 변환한 후 2D 공간 좌표를 픽셀 좌표로 변환하는 것을 래스터화라고 부른다. 래스터화는 보통 다음과 단계를 거친다.
- 클리핑 (Clipping)
- 원근 나누기 (Perspective division)
- 후면 제거 (Back-face culling)
- 뷰포트 변환 (Viewport transform)
- 스캔 변환 (Scan transform)
클리핑은 투영 변환 후�에 카메라 시점 바깥에 놓인 폴리곤을 잘라내는 작업을 말한다. 클리핑을 통해 불필요한 계산을 줄일 수 있다.
원근 나누기는 투영 변환 후에 2D 공간 좌표로 변환하는 작업을 말한다. 이 과정에서 카메라 시점에서 관찰한 물체의 깊이에 따라 크기를 조절하여 원근감을 만들어 낸다. 이때 x, y, z 좌표를 투영 변환을 통해 얻은 좌표인 4차원 좌표의 z 값으로 나누어 좌표를 변환한다.
후면 제거는 카메라 시점에서 보이지 않는 물체의 뒷면을 제거하는 작업을 말한다. 이 또한 클리핑 처럼 불필요한 계산을 줄일 수 있다.
뷰포트 변환은 2D 공간 좌표를 픽셀 좌표로 변환하는 작업을 말한다. 이 글에서는 뷰포트 변환을 통해 2D 공간 좌표를 CLI에서 표현할 수 있는 좌표로 변환한다.
스캔 변환은 픽셀 좌표로 변환한 후 좌표 사이를 채우는 작업을 말한다.
프래그먼트 처리
프래그먼트 처리는 래스터화를 통해 픽셀로 변환된 좌표를 처리하는 것이다. 이때 다양한 처리를 할 수 있다. 예를 들면 다음과 같은 것들이 있다.
- 조명 계산 (Lighting calculation)
- 텍스처 매핑 (Texture mapping)
- 알파 블렌딩 (Alpha blending)
여기서는 ASCII를 렌더링할 것이기 때문에 실제로 질감을 표현하기 위한 텍스처 매핑이나 투명도를 조절하는 알파 블렌딩은 처리하지 않을 것이다. 따라서 명암을 계산하기 위한 조명 계산만 필요하다.
조명 계산은 빛과 그림자를 이용하여 명암을 계산하는 것이다. 이때 빛과 그림자를 계산하기 위해서는 빛의 위치와 방향이 필요하다. 빛의 위치와 방향은 빛을 표현하는 좌표계를 구성한다. 이를 라이트 좌표계라고 부른다. 라이트 좌표계는 카메라 좌표계와 마찬가지로 빛의 위치와 방향을 표현하는 좌표계다.
구현하기
기본적인 렌더링 파이프라인 지식에 대해 알아보았으니 이제 이를 이용하여 ASCII로 3D 물체를 표현하는 렌더링 파이프라인을 구현해보자. 참고로 코드가 너무 길어 글에 다 담기 어렵기 때문에 필요한 부분만 설명하고 전체 코드는 GitHub 저장소 링크를 남길 것이다.
참고로 CLI 상에서 ASCII 만으로 표현하는 것이기 때문에 몇 가지 제약이 있다.
- 정확한 픽셀 좌표를 이용할 수 없다.
- 텍스처를 입힐 수 없다.
정확한 픽셀 좌표를 알더라도 CLI에서 표현할 수 없기 때문에 문자열 공간에 표현할 수 있는 좌표로 변환해야 한다. 여기서는 이차원 배열을 사용할 것이다. 또한 텍스처를 입힐 수 없기 때문에 명암을 표현할 때 사용할 문자열을 미리 정의할 필요가 있다. 이를 고려하여 구현해야 한다.
사전 준비
전반적으로 수학 계산이 필요하므로 이에 대한 객체를 먼저 만들어 보자.
class Matrix44 { /* ... */ }
class Vector2 { /* ... */ }
class Vector3 { /* ... */ }
class Vector4 { /* ... */ }여기서 자세한 코드는 적지 않지만 각 클래스는 기본적인 더하기 빼기 곱하기 나누기 연산을 포함하여 앞서 설명한 회전 변환, 크기 변환, 이동 변환 등을 처리할 수 있도록 구현해야 한다.
모델 로더 구현
모델 로더는 3D 모델 파일을 불러와서 버텍스와 폴리곤을 추출하는 역할을 한다. 여기서는 obj 확장자를 기준으로 구현할 것이다.
o Cube
v -1.000000 1.000000 1.000000
v -1.000000 -1.000000 1.000000
v -1.000000 1.000000 -1.000000
v -1.000000 -1.000000 -1.000000
v 1.000000 1.000000 1.000000
v 1.000000 -1.000000 1.000000
v 1.000000 1.000000 -1.000000
v 1.000000 -1.000000 -1.000000
f 5 3 1
f 3 8 4
f 7 6 8
f 2 8 6
f 1 4 2
f 5 2 6
f 5 7 3
f 3 7 8
f 7 5 6
f 2 4 8
f 1 3 4
f 5 1 2대부분의 obj 파일은 위와 같이 작성되어 있다 v는 버텍스를 나타내고 f는 Face element로 버텍스 연결을 통해 나타나는 도형을 뜻한다. 이를 이용하여 모델 로더를 구현해보자.
class Loader {
static loadFromFile(file: File): Promise<Polygon[]> {
/* ... */
}
static loadFromString(string: string): Polygon[] {
return this.parseOBJ(string);
}
private static parseOBJ(data: string): Polygon[] {
const lines = data.split("\n");
const vertices: Vector3[] = [];
const polygons: Polygon[] = [];
for (const line of lines) {
const parts = line.trim().split(" ");
if (parts[0] === "v") {
vertices.push(
new Vector3(
parseFloat(parts[1]),
parseFloat(parts[2]),
parseFloat(parts[3])
)
);
} else if (parts[0] === "f") {
polygons.push(
new Polygon([
vertices[parseInt(parts[1]) - 1],
vertices[parseInt(parts[2]) - 1],
vertices[parseInt(parts[3]) - 1],
])
);
}
}
return polygons;
}
}위 코드는 obj 내용을 파싱하여 버텍스와 폴리곤을 추출하는 역할을 한다. 코드 내용은 어렵지 않다. 단순히 whitespace를 기준으로 문자열을 나누고 값을 넣어줬을 뿐이다. 그리고 폴리곤 구성은 이미 정리한 버텍스 정보를 이용하여 만들었다.
렌더러 구현
이제 렌더러를 구현해보자. 렌더러는 다음과 같은 로직으로 구성된다.
- 광원과 카메라 위치를 정한다.
- 3D 모델을 불러온다.
- 모델의 버텍스에 월드 변환, 뷰 변환, 투영 변환을 한다.
- 래스터화를 통해 CLI에서 표현할 수 있는 좌표로 변환한다.
- 광원 위치를 기준으로 명암을 계산한다.
- 명암에 따른 ASCII 문자를 출력한다.
광원과 카메라는 아직 구현하지 않았으므로 먼저 각 변환에 대한 것을 구현해보자. 구현하다보면 카메라가 자연스럽게 구현될 것이다. 먼저 렌더러에 대한 기본 틀을 만들어보자.
export class ASCII3DRenderer {
el: HTMLElement;
width: number;
height: number;
frameBuffer: string[][];
depthBuffer: number[][];
private Shade = '.;ox%@';
constructor(_el: HTMLElement, width: number, height: number) {
this.el = _el;
this.width = width;
this.height = height;
this.frameBuffer = new Array(height + 1).fill(null).map(() => new Array(width + 1).fill(' '));
this.depthBuffer = new Array(height + 1).fill(null).map(() => new Array(width + 1).fill(255));
}
run() {
// FPS 계산 로직
}
private render() {
this.clearFrameBuffer();
this.process();
this.drawFrameBuffer();
}
private update() {
// ...
}
private process() {
// ...
}
private clearFrameBuffer() {
// 버퍼 초기화
}
private drawFrameBuffer() {
// 화면에 출력
}
}틀이라고 했지만 코드가 짧지는 않다. 클래스 내 각 필드는 렌더링에 필요한 정보를 담고 있다. el은 렌더링 결과를 출력할 엘리먼트, width와 height는 렌더링 결과의 크기, frameBuffer는 렌더링 결과를 담을 공간, depthBuffer는 깊이 버퍼로 렌더링 결과의 깊이를 담는다. 결과의 깊이라는 것은 카메라와의 거리를 말한다고 볼 수 있다.
그리고 여기서 Shade는 명암을 표현할 문자열을 미리 정의한 값이다.
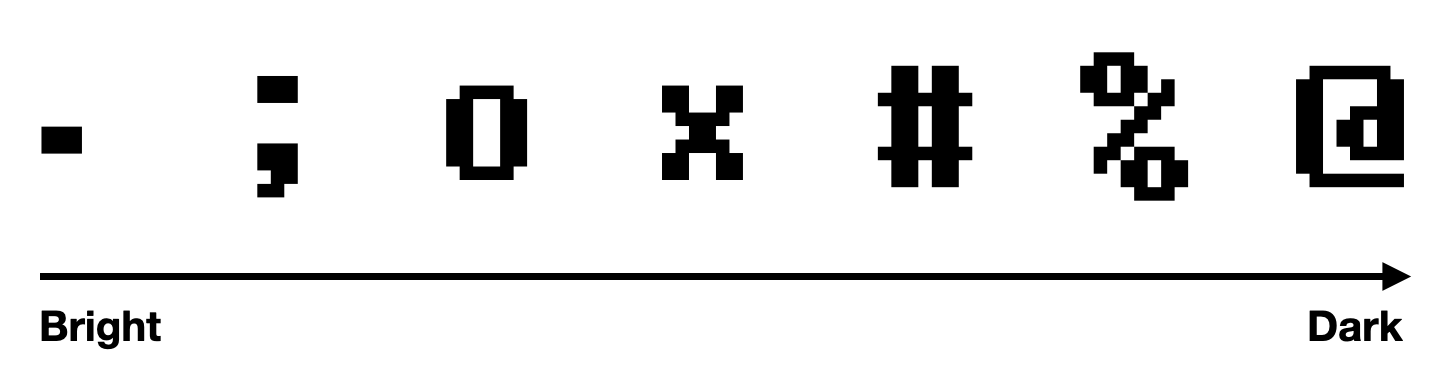
이어서 각 메서드를 보면 run 메서드는 60 프레임으로 렌더링을 유지하도록 하며 render 메서드는 그려진 것을 지우고 파이프라인 결과를 그리면서 렌더링을 처리한다. process 메서드는 버텍스 처리, 래스터화 등 렌더링 파이프라인 작업을 수행한다. 이 부분을 채우면 사실상 완성이라 할 수 있다. process 메서드는 다음과 같이 진행될 것이다.
- 카메라의 위치와 방향을 정한다.
- 오브젝트에 월드 변환을 적용한다.
- 오브젝트에 뷰 변환을 적용한다.
- 오브젝트에 투영 변환을 적용한다.
- 래스터화를 통해 CLI에�서 표현할 수 있는 좌표로 변환한다.
- 명암에 따른 ASCII 문자를 출력한다.
오브젝트 설정
카메라를 구현하기 전에 먼저 렌더러에 렌더링할 오브젝트를 추가해보자. 오브젝트는 다음과 같은 일을 할 수 있다.
obj파일을 통해 폴리곤 메시를 불러올 수 있다.- 스스로 회전, 이동, 크기를 가진다 할 수 있다.
- 행렬 연산을 통해 버텍스를 변환할 수 있다.
먼저 오브젝트 클래스를 만들어보자.
export class Object {
mesh: Polygon[]; // 폴리곤 메시
position: Vector3; // 위치
rotate: Vector3; // 회전
scale: Vector3; // 크기
constructor() {
// 초기화
this.mesh = [];
this.position = new Vector3(0, 0, 0);
this.rotate = new Vector3(0, 0, 0);
this.scale = new Vector3(1, 1, 1);
}
// obj 파일로부터 폴리곤 메시를 불러온다
async loadFromFile(file: File) {
this.mesh = await Loader.loadFromFile(file);
}
// obj 문자열로부터 폴리곤 메시를 불러온다
async loadFromString(string: string) {
this.mesh = await Loader.loadFromString(string);
}
// 프레임마다 오브젝트를 변화시킬 수 있는 메서드
update() {
// override this method
}
// 월드 변환
transform(v: Vector4) {
const matrix = Matrix44.identity()
.multiply(Matrix44.rotateX(this.rotate.x))
.multiply(Matrix44.rotateY(this.rotate.y))
.multiply(Matrix44.rotateZ(this.rotate.z))
.multiply(Matrix44.scale(this.scale))
.multiply(Matrix44.translate(this.position));
return v.transform(matrix);
}
/* Setter */
setTranslate(v: Vector3) {
this.position = v;
}
setScale(v: Vector3) {
this.scale = v;
}
setRotateX(angle: number) {
this.rotate.x = angle;
}
setRotateY(angle: number) {
this.rotate.y = angle;
}
setRotateZ(angle: number) {
this.rotate.z = angle;
}
}위 코드는 Object 클래스를 구현한 것이다. Object는 mesh 필드에 폴리곤 메시를 가지며 position, rotate, scale 필드에 각각 위치, 회전, 크기를 가진다. 또한 loadFromFile과 loadFromString 메서드를 통해 obj 파일을 불러와 폴리곤 메시를 설정할 수 있다. 그리고 transform 메서드를 통해 버텍스를 변환할 수 있다.
참고로 버텍스를 변환하는 행렬은 단위 행렬에 회전, 크기, 이동 변환 행렬을 곱한 행렬이다.
이어서 update 메서드는 프레임마다 오브젝트를 변화시킬 수 있는 메서드이다. 이 메서드는 오버라이드하여 사용할 수 있다. 그리고 setTranslate, setScale, setRotateX, setRotateY, setRotateZ 메서드를 통해 각각 위치, 크기, 회전을 설정할 수 있다. update 메서드를 보면 알겠지만 기본적으로 Object 클래스는 상속해서 사용할 수 있다.
이제 렌더러에도 오브젝트를 추가할 수 있도록 코드를 수정해보자.
export class ASCII3DRenderer {
objects: Object[] = [];
placeObject(object: Object) {
this.objects.push(object);
}
// ...
}이제 기본적인 오브젝트 구현과 렌더러에 오브젝트를 추가하는 것까지 구현했다. 이제 버텍스 처리 과정을 구현해보자.
버텍스 처리
버텍스 처리는 오브젝트의 버텍스에 대해 월드 변환, 뷰 변환, 투영 변환을 적용하는 것이다. 먼저 렌더러가 가진 오브젝트에 월드 변환을 적용해보자.
export class ASCII3DRenderer {
// ...
private process() {
for (const object of this.objects) {
for (const polygon of object.mesh) {
// 4x4 행렬 연산을 위해 Vector4로 변환
let v1 = new Vector4(polygon.vertices[0].x, polygon.vertices[0].y, polygon.vertices[0].z, 1);
let v2 = new Vector4(polygon.vertices[1].x, polygon.vertices[1].y, polygon.vertices[1].z, 1);
let v3 = new Vector4(polygon.vertices[2].x, polygon.vertices[2].y, polygon.vertices[2].z, 1);
// 월드 변환
v1 = object.transform(v1);
v2 = object.transform(v2);
v3 = object.transform(v3);
// ...
}
}
}
}먼저 4x4 행렬 연산을 해야하기 때문에 오브젝트의 폴리곤을 순회하며 각 버텍스를 4차원 좌표로 변환한다. 그리고 object.transform 메서드를 통해 각 버텍스에 월드 변환을 적용한다. 계산 함수는 앞서 구현을 마쳤기 때문에 간단하게 적용할 수 있다. 이제 뷰 변환을 적용해보자. 뷰 변환을 위해선 카메라를 먼저 구현해야 하므로 Camera 클래스를 만들어보자.
export class Camera {
eye: Vector3; // 카메라의 위치
look: Vector3; // 카메라가 바라보는 방향
up: Vector3; // 카메라의 상단 방향
rotate: Vector3; // 카메라의 회전 각도
constructor() {
// 카메라의 초기 위치, 방향, 상단 방향, 회전 각도를 설정
this.eye = new Vector3(0, 0, 0);
this.look = new Vector3(0, 0, 1);
this.up = new Vector3(0, 1, 0);
this.rotate = new Vector3(0, 0, 0); // x, y, z 축을 중심으로 회전 각도를 나타낸다
}
transform(v: Vector4) {
// 카메라의 전방, 오른쪽, 상단 벡터를 계산
const forward = this.look.subtract(this.eye).normalize();
const newUp = forward.cross(this.up).normalize();
const right = newUp.cross(forward);
const matrix = new Matrix44(
right.x, right.y, right.z, 0,
newUp.x, newUp.y, newUp.z, 0,
forward.x, forward.y, forward.z, 0,
this.eye.x, this.eye.y, this.eye.z, 1
);
return v.transform(matrix);
}
}위 코드는 Camera 클래스를 구현한 것으로 eye, look, up, rotate 필드를 가진다. 각 필드는 카메라의 위치, 방향, 업 벡터, 회전을 나타낸다. 그리고 transform 메서드를 통해 뷰 변환을 적용할 수 있다. 구현을 살펴보면 월드 변환보다 복잡하다는 것을 알 수 있다. 하나씩 살펴보자.
순서대로 나오는 forward, newUp, right는 전방 벡터, 오른쪽 벡터, 상단 벡터를 말하고 각 벡터는 카메라의 방향과 위치를 나타내는 데 사용된다.
- 전방 벡터(Forward Vector): 카메라의 위치와 바라보는 방향을 뺀 벡터를 정규화한 것이다. 이 벡터는 카메라의 전방 방향을 나타내며, 물체의 깊이를 나타내는 데 사용된다.
- 오른쪽 벡터(Right Vector): 전방 벡터와 상단 벡터의 외적을 정규화한 것이다. 이 벡터는 카메라의 오른쪽 방향을 나타내며, 물체의 좌우 이동이나 회전을 구현하는 데 사용된다.
- 상단 벡터(Up Vector): 오른쪽 벡터와 전방 벡터의 외적을 정규화한 것이다. 이 벡터는 카메라의 상단 방향을 나타내며, 물체의 상하 이동을 구현하는 데 사용된다.
여기서 벡터의 정규화란 벡터의 방향을 그대로 두고 벡터의 크기를 1로 만드는 것을 말한다. 이렇게 구한 ��벡터들을 이용하여 뷰 변환 행렬을 만들어 버텍스에 적용한다. 이제 렌더러에 카메라를 추가하고 뷰 변환을 적용해보자.
export class ASCII3DRenderer {
// ...
camera: Camera = new Camera();
private process() {
this.camera.eye = new Vector3(0, 0, -3);
for (const object of this.objects) {
for (const polygon of object.mesh) {
// 4x4 행렬 연산을 위해 Vector4로 변환
let v1 = new Vector4(polygon.vertices[0].x, polygon.vertices[0].y, polygon.vertices[0].z, 1);
let v2 = new Vector4(polygon.vertices[1].x, polygon.vertices[1].y, polygon.vertices[1].z, 1);
let v3 = new Vector4(polygon.vertices[2].x, polygon.vertices[2].y, polygon.vertices[2].z, 1);
// 월드 변환
v1 = object.transform(v1);
v2 = object.transform(v2);
v3 = object.transform(v3);
// 뷰 변환
v1 = this.camera.transform(v1);
v2 = this.camera.transform(v2);
v3 = this.camera.transform(v3);
// ...
}
}
}
}이제 투영 변환만 남았다. 투영 변환을 해줄 Projection 클래스를 만들어보자.
export class Projection {
fov: number;
aspect: number;
near: number;
far: number;
constructor(fov: number, aspect: number, near: number, far: number) {
this.fov = fov;
this.aspect = aspect;
this.near = near;
this.far = far;
}
transform(v: Vector4) {
const fovRad = this.fov * (Math.PI / 180);
const f = 1.0 / Math.tan(fovRad / 2);
const rangeInv = 1.0 / (this.near - this.far);
// prettier-ignore
const matrix = new Matrix44(
f / this.aspect, 0, 0, 0,
0, f, 0, 0,
0, 0, (this.near + this.far) * rangeInv, -1,
0, 0, this.near * this.far * rangeInv * 2, 0
);
const transformed = v.transform(matrix);
transformed.x /= transformed.w;
transformed.y /= transformed.w;
transformed.z /= transformed.w;
return transformed;
}
}위 코드는 Projection 클래스를 구현한 것으로 fov, aspect, near, far 필드를 가진다. 각 필드는 시야각, 종횡비, 가까운 면, 먼 면을 나타낸다. 그리고 transform 메서드를 통해 투영 변환을 적용할 수 있다. 공식에 대한 설명은 조금 복잡하므로 여기서는 생략한다. 이제 렌더러에 투영 변환을 적용해보자.
export class ASCII3DRenderer {
// ...
projection: Projection;
constructor(_el: HTMLElement, width: number, height: number) {
// ...
this.projection = new Projection(70, width / 2 / height, 0.1, 100);
}
private process() {
this.camera.eye = new Vector3(0, 0, -3);
for (const object of this.objects) {
for (const polygon of object.mesh) {
// 4x4 행렬 연산을 위해 Vector4로 변환
let v1 = new Vector4(polygon.vertices[0].x, polygon.vertices[0].y, polygon.vertices[0].z, 1);
let v2 = new Vector4(polygon.vertices[1].x, polygon.vertices[1].y, polygon.vertices[1].z, 1);
let v3 = new Vector4(polygon.vertices[2].x, polygon.vertices[2].y, polygon.vertices[2].z, 1);
// 월드 변환
v1 = object.transform(v1);
v2 = object.transform(v2);
v3 = object.transform(v3);
// 뷰 변환
v1 = this.camera.transform(v1);
v2 = this.camera.transform(v2);
v3 = this.camera.transform(v3);
// 투영 변환
v1 = this.projection.transform(v1);
v2 = this.projection.transform(v2);
v3 = this.projection.transform(v3);
}
}
}
}여기까지 왔다면 버텍스 처리 과정은 끝났다.
래스터화
지금까지 출력된 결과물을 보지 못했기 때문에 지겨울 수 있다. 지금부터 구현할 래스터화를 마치며 실제 결과물을 확인할 수 있게 될 것이다. 더 지겨워지기 전에 가볍게 버텍스가 가진 세 개의 좌표를 선으로 연결해보자.
export class ASCII3DRenderer {
private process() {
this.camera.eye = new Vector3(0, 0, -3);
for (const object of this.objects) {
for (const polygon of object.mesh) {
// ...
// 래스터화
this.rasterize(v1, v2, v3);
}
}
}
private rasterize(v1: Vector4, v2: Vector4, v3: Vector4) {
// 점들을 화면 좌표로 변환
const p1 = new Vector2(((v1.x + 1) * this.width) / 2, ((1 - v1.y) * this.height) / 2);
const p2 = new Vector2(((v2.x + 1) * this.width) / 2, ((1 - v2.y) * this.height) / 2);
const p3 = new Vector2(((v3.x + 1) * this.width) / 2, ((1 - v3.y) * this.height) / 2);
// 선 그리기
this.drawLine(p1, p2);
this.drawLine(p2, p3);
this.drawLine(p3, p1);
}
private drawLine(p1: Vector2, p2: Vector2) {
const result = p2.subtract(p1);
const len = result.length();
const normalized = result.normalize();
for (let i = 0; i < len; i++) {
const current = normalized.multiply(i);
const p = p1.add(current);
// 화면을 벗어나는 좌표는 무시
if (p.x >= 0 && p.x < this.width && p.y >= 0 && p.y < this.height) {
this.frameBuffer[Math.floor(p.y)][Math.floor(p.x)] = '#';
}
}
}
}위 코드에서 rasterize 메서드는 버텍스를 화면 좌표로 변환하고 drawLine 메서드를 통해 선을 그려준다. drawLine 메서드는 두 점 사이의 거리를 구하고 해당하는 좌표에 '#'을 넣어준다. 이제 렌더러에 오브젝트를 추가하고 렌더링을 해보자. 여기서는 Cube 오브젝트를 만들어서 추가해볼 것이다.
import { Vector3 } from '../math';
import { Object } from '../object';
export class Cube extends Object {
angle = 0;
constructor() {
super();
this.loadFromString(mesh);
}
override update(): void {
this.setRotateX(-this.angle * 2);
this.setRotateY(-this.angle * 2);
this.setRotateZ(-this.angle);
this.setTranslate(new Vector3(0, 0, -5));
this.angle += 0.007;
}
}
export const mesh = /* obj 파일 내용 */;위 코드를 보면 angle을 통해 프레임마다 오브젝트를 회전시키도록 만들었다는 것을 알 수 있다. 이제 렌더러에 추가하고 렌더링을 해보자. 코드가 꼭 다음과 같을 필요는 없다.
const renderer = new ASCII3DRenderer(document.getElementById('app'), 150, 50);
const cube = new Cube();
renderer.placeObject(cube);
renderer.run();위와 같이 구현했다면 브라우저에서 렌더링 결과를 확인할 수 있다. 렌더링 결과를 한 번 살펴보자.
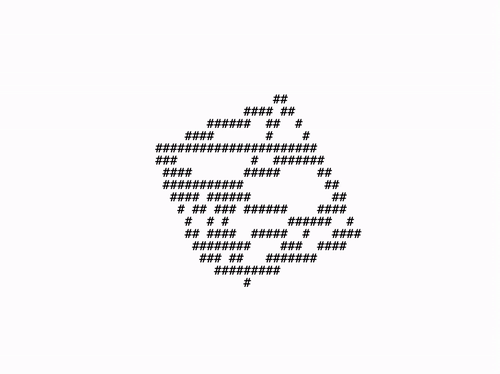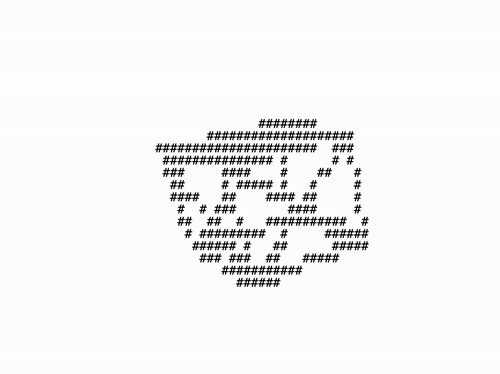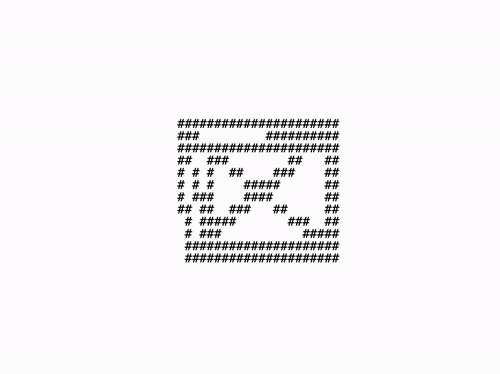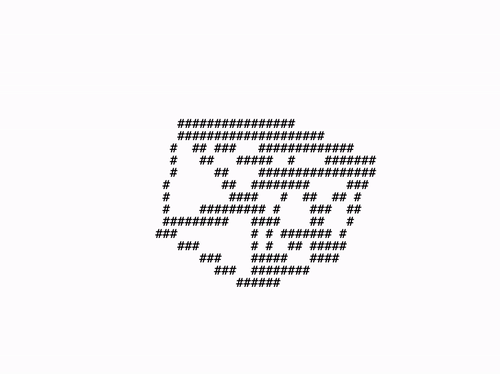
조금 어색하지만 큐브가 회전하는 것처럼 보이긴한다. 이번에는 버텍스 사이를 채워보자.
export class ASCII3DRenderer {
private process() {
this.camera.eye = new Vector3(0, 0, -3);
for (const object of this.objects) {
for (const polygon of object.mesh) {
// ...
// 래스터화
this.rasterize(v1, v2, v3);
}
}
}
private rasterize(v1: Vector4, v2: Vector4, v3: Vector4) {
// 점들을 화면 좌표로 변환
const p1 = new Vector2(((v1.x + 1) * this.width) / 2, ((1 - v1.y) * this.height) / 2);
const p2 = new Vector2(((v2.x + 1) * this.width) / 2, ((1 - v2.y) * this.height) / 2);
const p3 = new Vector2(((v3.x + 1) * this.width) / 2, ((1 - v3.y) * this.height) / 2);
// 삼각형의 경계 박스 계산
const minX = Math.floor(Math.max(0, Math.min(p1.x, p2.x, p3.x)));
const minY = Math.floor(Math.max(0, Math.min(p1.y, p2.y, p3.y)));
const maxX = Math.floor(Math.min(this.width, Math.max(p1.x, p2.x, p3.x)));
const maxY = Math.floor(Math.min(this.height, Math.max(p1.y, p2.y, p3.y)));
for (let x = minX; x <= maxX; x++) {
for (let y = minY; y <= maxY; y++) {
const p = new Vector2(x, y);
// 삼각형 내부에 있다면
if (this.isPointInTriangle(p, p1, p2, p3)) {
this.setPixel(x, y);
}
}
}
}
private isPointInTriangle(p: Vector2, p1: Vector2, p2: Vector2, p3: Vector2): boolean {
// 세 개의 부분 삼각형의 부호 계산
const b1 = this.sign(p, p1, p2) < 0;
const b2 = this.sign(p, p2, p3) < 0;
const b3 = this.sign(p, p3, p1) < 0;
// 모든 부분 삼각형의 부호가 같으면 삼각형 내부에 있는 것으로 간주
return b1 === b2 && b2 === b3;
}
// ...
}삼각형 내부도 채워진 것을 확인할 수 있다. 이제 drawLine 메서드는 사용하지 않는다. 참고로 명암이 없는 큐브는 어색하게 보이기 때문에 대신 소 오브젝트를 렌더링했다.

광원 계산
마지막으로 명암을 넣어보자. 이를 위해선 광원을 추가해야 한다.
export class ASCII3DRenderer {
// ...
private process() {
this.camera.eye = new Vector3(0, 0, -2);
for (const object of this.objects) {
for (const polygon of object.mesh) {
// 4x4 행렬 연산을 위해 Vector4로 변환
let v1 = new Vector4(polygon.vertices[0].x, polygon.vertices[0].y, polygon.vertices[0].z, 1);
let v2 = new Vector4(polygon.vertices[1].x, polygon.vertices[1].y, polygon.vertices[1].z, 1);
let v3 = new Vector4(polygon.vertices[2].x, polygon.vertices[2].y, polygon.vertices[2].z, 1);
// 월드 변환
v1 = object.transform(v1);
v2 = object.transform(v2);
v3 = object.transform(v3);
// 뷰 변환
v1 = this.camera.transform(v1);
v2 = this.camera.transform(v2);
v3 = this.camera.transform(v3);
// 광원 계산
const brightness = this.calculateLight(v1, v2, v3);
// 투영 변환
v1 = this.projection.transform(v1);
v2 = this.projection.transform(v2);
v3 = this.projection.transform(v3);
// 래스터화
this.rasterize(v1, v2, v3, brightness);
}
}
}
private calculateLight(v1: Vector4, v2: Vector4, v3: Vector4): number {
// 광원의 방향 벡터
// 카메라가 바라보는 방향 (0, 0, 1)을 사용함
const lightDirection = new Vector3(0, 0, 1).normalize();
// 삼각형의 표면 법선 벡터 계산
const normal = this.calculateSurfaceNormal(
new Vector3(v1.x, v1.y, v1.z),
new Vector3(v2.x, v2.y, v2.z),
new Vector3(v3.x, v3.y, v3.z)
);
// 광원과 표면 법선 벡터 간의 각도 계산
const cosAngle = normal.dot(lightDirection);
// 광원 각도에 따라 픽셀의 밝기 결정
const brightness = Math.max(0, cosAngle);
return brightness;
}
private calculateSurfaceNormal(v1: Vector3, v2: Vector3, v3: Vector3): Vector3 {
// 두 변을 정의
const edge1 = v3.subtract(v2);
const edge2 = v1.subtract(v3);
// 외적을 계산하여 표면 법선 벡터 반환
return edge1.cross(edge2).normalize();
}
// ...
}광원 계산은 뷰 변환과 투영 변환 사이에 이루어져야 한다. 투영 변환을 마친 후에는 이미 2D 공간 좌표로 변환된 이후기 때문에 그 전에 처리하는 것이 맞다. 이어서 위 코드에서 calculateLight 메서드는 광원의 방향 벡터와 삼각형의 표면 법선 벡터를 이용하여 광원과 표면 법선 벡터 간의 각도를 계산한다. 참고로 법선 벡터란 평면의 방향을 나타내는 벡터이다. 이를 이용하여 광원의 각도에 따라 픽셀의 밝기를 결정한다.
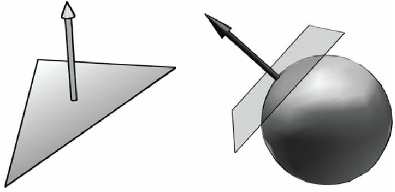
이제 명암에 따라 ASCII 문자를 출력해보자.
export class ASCII3DRenderer {
// ...
private process() {
this.camera.eye = new Vector3(0, 0, -2);
for (const object of this.objects) {
for (const polygon of object.mesh) {
// 4x4 행렬 연산을 위해 Vector4로 변환
let v1 = new Vector4(polygon.vertices[0].x, polygon.vertices[0].y, polygon.vertices[0].z, 1);
let v2 = new Vector4(polygon.vertices[1].x, polygon.vertices[1].y, polygon.vertices[1].z, 1);
let v3 = new Vector4(polygon.vertices[2].x, polygon.vertices[2].y, polygon.vertices[2].z, 1);
// 월드 변환
v1 = object.transform(v1);
v2 = object.transform(v2);
v3 = object.transform(v3);
// 뷰 변환
v1 = this.camera.transform(v1);
v2 = this.camera.transform(v2);
v3 = this.camera.transform(v3);
// 광원 계산
const brightness = this.calculateLight(v1, v2, v3);
// 투영 변환
v1 = this.projection.transform(v1);
v2 = this.projection.transform(v2);
v3 = this.projection.transform(v3);
// 래스터화
this.rasterize(v1, v2, v3, brightness);
}
}
}
private rasterize(v1: Vector4, v2: Vector4, v3: Vector4, brightness: number) {
// 점들을 화면 좌표로 변환
const p1 = new Vector2(((v1.x + 1) * this.width) / 2, ((1 - v1.y) * this.height) / 2);
const p2 = new Vector2(((v2.x + 1) * this.width) / 2, ((1 - v2.y) * this.height) / 2);
const p3 = new Vector2(((v3.x + 1) * this.width) / 2, ((1 - v3.y) * this.height) / 2);
// 삼각형의 경계 박스 계산
const minX = Math.floor(Math.max(0, Math.min(p1.x, p2.x, p3.x)));
const minY = Math.floor(Math.max(0, Math.min(p1.y, p2.y, p3.y)));
const maxX = Math.floor(Math.min(this.width, Math.max(p1.x, p2.x, p3.x)));
const maxY = Math.floor(Math.min(this.height, Math.max(p1.y, p2.y, p3.y)));
// 박스 내부 순회
for (let y = minY; y <= maxY; y++) {
for (let x = minX; x <= maxX; x++) {
// 화면 밖이라면 무시
if (x < 0 || x >= this.width || y < 0 || y >= this.height) {
continue;
}
const p = new Vector2(x, y);
// 삼각형 내부에 있다면
if (this.isPointInTriangle(p, p1, p2, p3)) {
// 더 낮은 깊이라면 덮어쓴다
if ((v1.w + v2.w + v3.w) / 3.0 <= this.depthBuffer[y][x]) {
const shade = this.Shade[Math.round(brightness * (this.Shade.length - 1))];
this.frameBuffer[y][x] = shade;
this.depthBuffer[y][x] = (v1.w + v2.w + v3.w) / 3.0;
}
}
}
}
}
// ...
}명암은 brightness 값에 따라 Shade 단계를 선택한다. 그리고 여기서 depthBuffer가 처음으로 등장하는데, 이는 깊이 버퍼를 의미한다. 깊이 버퍼는 화면에 그려진 픽셀의 깊이를 저장하는 버퍼로, 더 낮은 깊이를 가진 픽셀이 더 앞에 있다는 것을 의미한다. 이를 통해 뒤에 있는 픽셀이 앞에 있는 픽셀을 덮어쓰지 않도록 한다.

확장 아스키 사용
여기까지 왔다면 완성했다고 볼 수 있다. 여기서 조금만 수정해서 명암이 더 대비되도록 만들어보자. 확장 아스키를 사용하면 구현할 수 있다.

어려울 것 없이 Shade 배열을 수정하면 된다.
private Shade = '·┼╬░▒▓█';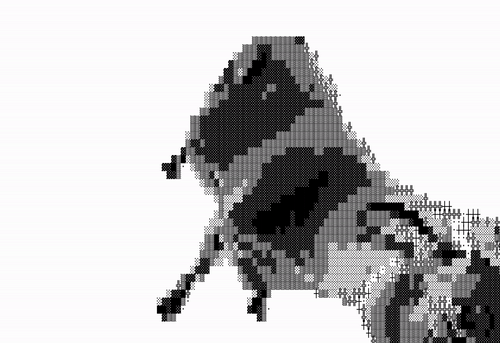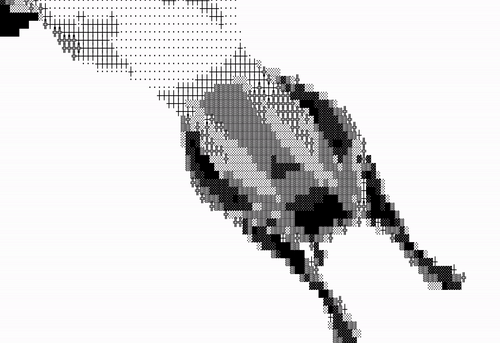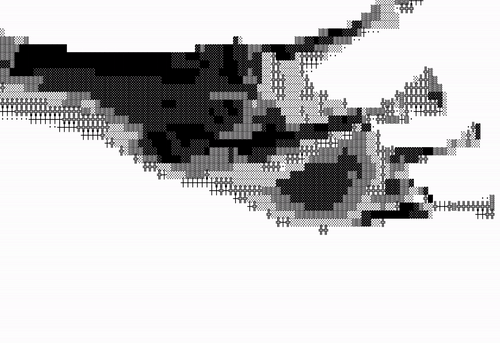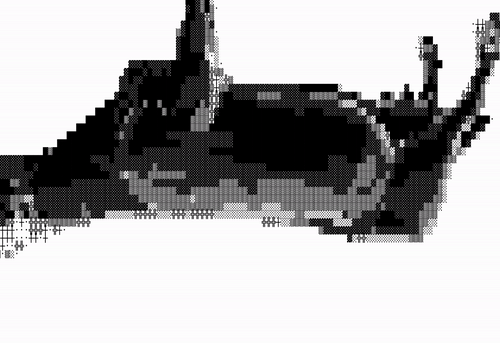
마치며
JavaScript(TypeScript를 빌드)로 구현했기 때문에 웹에서 실행이 가능하다. 결과적으로 다음과 같이 결과물을 웹에서 볼 수 있다.
별도로 배포한 Chromatic에서 보면 더 다양한 예제를 볼 수 있다.
반쯤 재미로 시작한 프로젝트지만 생각보다 구현이 쉽지는 않았다. 게임 개발이 하고 싶어 개발자의 길을 걸었지만 마지막으로 게임 개발과 관련된 공부를 한지도 벌써 10년이 지났다. 그럼에도 불구하고 오랜만에 작업을 하니 재미있었고 다시 머리가 깨어나는 느낌이었다. 역시 학습에서 중요한 것은 평소에 잘 하지 않는 것을 해보는 것, 그리고 그것을 익숙해질 때까지 반복하는 것이라는 것을 다시 한 번 깨달았다. 다음에 기회가 된다면 또 다시 이런 재미있는 프로젝트를 해보고 싶다.
